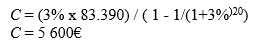Lorsque sonne l’heure de la retraite, que l’on a perçu le capital de ses assurances et que l’on s’est constitué un portefeuille pour ses vieux jours, comment estimer le revenu que l’ensemble de ce patrimoine peut générer après la pension pour répondre à ses besoins en fonction des attentes, d’une certaine durée et de l’aversion au risque ?
Quatre variables
Serge Wibaut, Economiste, nous propose quatre formules utiles lorsque l’on cherche à estimer le montant des flux monétaires qu’un fonds, ou un ensemble d’avoirs financiers, peut générer annuellement. A vos calculettes !
Le calcul de ces flux, que l’on nomme annuités, dépend de quatre variables :
V : la valeur actuelle, ou présente, du portefeuille
r : le rendement attendu sur la période sous considération
T : l’horizon de temps (par exemple, l’espérance de vie)
g : le taux auquel l’annuité peut être requise de croître (pour se protéger contre l’inflation par exemple)
Analysons ces quatre cas de figure.
La perpétuité
On suppose ici que le portefeuille doit générer une annuité constante, notée C, jusqu’à la nuit des temps (T vaut donc l’infini). Cette hypothèse n’est pas aussi absurde qu’il n’y paraît si, par exemple, le propriétaire du fonds ou du portefeuille considère que ses avoirs doivent générer des revenus pour sa descendance.
Dans ce cas, l’annuité est donnée par :
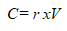
Pour un capital de 100.000 euros, l’annuité constante se calcule comme suit :
V = 100 000 €, pour un rendement estimé r=3%
L’annuité constante C sera donc de 3.000€ soit 250 euros par mois.
La perpétuité croissante
On demande ici que l’annuité croisse d’année en année d’un taux égal à g%.
Dans ce cas, l’annuité en première année est donnée par
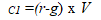
L’annuité en deuxième année est égale à C2 = C1 x (1+g) et ainsi de suite.
Pour un portefeuille de 100.000 euros l’annuité croissante sera donc de :
V = 100 000€, r=3% et g=2%
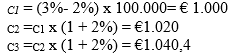
Etc.
L’annuité constante
Il s’agit de déterminer quel flux annuel le fonds ou le portefeuille peut générer pendant T années (et T n’est pas égal à l’infini comme dans les deux cas précédents) avant d’être épuisé. On suppose ici que ce flux est constant à travers le temps.
Dans ce cas, l’annuité est donnée par :
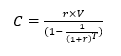
Pour un capital de 100.000 euros, l’annuité constante sera calculée de la façon suivante :

L’annuité à taux croissant
On se trouve dans la même situation qu’au cas précédent si ce n’est que l’on veut voir l’annuité croître d’un taux de g% au fil du temps.
L’annuité prend alors une forme un peu plus compliquée, à savoir :
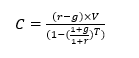
Ce qui donne pour un portefeuille de 100.000 euros, les montants suivants :
V = 100.000 €, r=3%, T= 20 ans et g = 2%
La première annuité vaut alors :
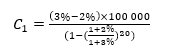
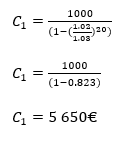
La deuxième annuité sera donnée par C2 = C1 x (1+2%) = 5.763€ et ainsi de suite pour les années suivantes.
Un cas particulier des annuités consiste en ce que le portefeuille ne soit pas totalement épuisé au bout des T années mais qu’il subsiste un montant préalablement défini (ce montant pourrait correspondre à un héritage ou à un matelas de sécurité).
Il faudra alors calculer la valeur présente de ce montant (à savoir la valeur du montant à investir aujourd’hui à du r% pour obtenir au bout de T années le montant requis) et soustraire cette valeur à la valeur totale V. Le résultat de cette soustraction livre le montant d’argent devant générer des annuités pendant T années.
Exemple dans le cas d’une annuité constante pour un capital de 100.000€, r=3%, T= 20 ans et on souhaite que 30.000 € demeurent dans le fond au bout des 20 années considérées.
La valeur présente des 30.000 € placés à du 3% pendant 20 ans est donnée par :
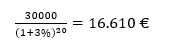
Ceci signifie que 16.610 € placés aujourd’hui à du 3% pendant 20 ans vaudront alors 30.000 €.
Il reste donc aujourd’hui 100.000€ – 16.610€ = 83.390€ pour générer une annuité constante pendant 20 ans. Cette annuité est calculée grâce à la formule :