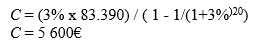Wanneer het tijd is om met pensioen te gaan, wanneer je het kapitaal van je verzekeringspolissen hebt verzameld en een portefeuille hebt opgebouwd voor je oude dag, hoe schat je dan het inkomen in dat al dit vermogen na je pensionering kan genereren om aan je behoeften te voldoen, afhankelijk van je verwachtingen, een bepaalde periode en je risicotolerantie?
Vier variabelen
Econoom Serge Wibaut stelt vier handige formules voor om in te schatten hoeveel cashflow een fonds, of een groep financiële activa, elk jaar kan genereren. Houd je rekenmachine gereed!
De berekening van deze stromen, bekend als annuïteiten, hangt af van vier variabelen:
V: de huidige waarde van de portefeuille
r : het verwachte rendement over de beschouwde periode
T : tijdshorizon (bijv. levensverwachting)
g: het percentage waarmee de lijfrente mogelijk moet stijgen (bijvoorbeeld ter bescherming tegen inflatie)
Laten we deze vier scenario’s eens bekijken.
Levenslang
Er wordt aangenomen dat de portefeuille een constante annuïteit, C, zou moeten genereren tot het einde der tijden(T is dus oneindig). Deze veronderstelling is niet zo absurd als het lijkt, bijvoorbeeld als de eigenaar van het fonds of de portefeuille van mening is dat zijn vermogen inkomsten moet genereren voor zijn nakomelingen.
In dit geval wordt de annuïteit gegeven door:
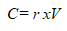
Voor een kapitaal van 100.000 euro wordt de constante annuïteit als volgt berekend:
V = €100.000, voor een geschatte opbrengst r=3%
De constante annuïteit C zal dus €3.000 zijn, of €250 per maand.
Op de groei
Hier vragen we dat de annuïteit van jaar tot jaar groeit met een percentage dat gelijk is aan g%.
In dit geval wordt de jaarlijkse afbetaling in het eerste jaar gegeven door
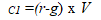
De jaarlijkse betaling in het tweede jaar is gelijk aan C2 =C1 x (1+g) enzovoort.
Voor een portefeuille van 100.000 euro zal de toenemende jaarlijkse afbetaling dus :
V = €100.000, r=3% en g=2%
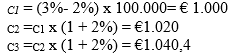
Etc.
Constante annuïteit
Het doel is om te bepalen hoeveel jaarlijkse kasstroom het fonds of de portefeuille kan genereren gedurende T jaar (en T is niet gelijk aan oneindig, zoals in de vorige twee gevallen) voordat het uitgeput is. Er wordt aangenomen dat deze stroom constant is in de tijd.
In dit geval wordt de annuïteit gegeven door:
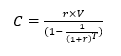
Voor een kapitaal van 100.000 euro wordt de constante annuïteit als volgt berekend:

Lijfrente met stijgende rente
We bevinden ons in dezelfde situatie als in het vorige geval, behalve dat we willen dat de annuïteit in de loop van de tijd stijgt met een percentage van g%.
De annuïteit neemt dan een iets ingewikkelder vorm aan:
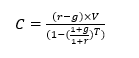
Voor een portefeuille van 100.000 euro geeft dit de volgende bedragen:
V = €100.000, r=3%, T= 20 jaar en g = 2%
De eerste jaarlijkse termijn is dan:
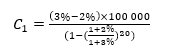
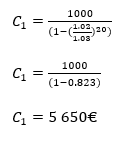
De tweede jaarlijkse storting wordt gegeven door C2 = C1 x (1+2%) x (1+2%) = €5.763 enzovoort voor de volgende jaren.
Een speciaal geval van annuïteiten is dat de portefeuille niet volledig uitgeput is aan het einde van de T-jaren, maar dat er een vooraf bepaald bedrag overblijft (dit bedrag kan overeenkomen met een erfenis of een veiligheidsbuffer).
Vervolgens moeten we de contante waarde van dit bedrag berekenen (d.w.z. de waarde van het bedrag dat vandaag tegen r% moet worden geïnvesteerd om het vereiste bedrag aan het einde van T jaar te verkrijgen) en deze waarde aftrekken van de totale waarde V. Het resultaat van deze aftrekking is het bedrag dat annuïteiten moet genereren over T jaar. Het resultaat van deze aftrekking is het bedrag dat annuïteiten moet genereren over T jaar .
Bijvoorbeeld, in het geval van een constante annuïteit voor een kapitaal van €100.000, r=3%, T= 20 jaar en we willen dat er €30.000 in het fonds overblijft aan het einde van de 20 jaar in kwestie.
De contante waarde van €30.000 geïnvesteerd tegen 3% gedurende 20 jaar wordt gegeven door:
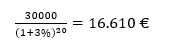
Dit betekent dat €16.610, vandaag belegd tegen 3% gedurende 20 jaar, dan €30.000 waard zal zijn.
Dan blijft er € 100.000 – € 16.610 = € 83.390 over voor een constante jaarlijkse betaling gedurende 20 jaar. Deze annuïteit wordt berekend met de formule: